| Isostasy and gravitational forceS... | ||||||||
| Exercise: A reference lithosphere is zl km thick and includes a zc km thick continental crust. This reference lithosphere is in isostatic and mechanical equilibrium and has a surface elevation hc at sea level (hc=0 m). An episode of lithospheric deformation changes the thickness of the crust and that of the entire lithosphere.
a/ (10 marks) Give the surface elevation h of the deformed lithosphere as a function of the densities and thicknesses of the crust and lithospheric mantle of the reference lithosphere, fc the thickening/thinning factor of the crust, fl the thickening/thinning factor of the entire lithosphere, and any other relevant parameters. Please note that the surface elevation h for thickening (fc and fl >1) and thinning (fc and fl <1) must be considered separately. b/ (12 marks) Numerical applications (Use the parameter values given below): Calculate h, GPE, Δ GPE (ie, the gravitational force Fg) for the three following cases: c/ (3 marks) The gravitational force acts on a vertical lithospheric section down to the compensation level. The gravitational stress is given by the ratio between the gravitational force and the surface area on which the force is applied. Assuming lithospheric rocks have a depth independent strength of 70MPa, would the gravitational forces determined in b/ produce any lithospheric deformation? NB: 5 marks are attributed to the explanation and the overall quality of the report.
|
||||||||
| hc: elevation of the initial lithosphere=0 m; zl: thickness of the continental lithosphere near thermal equilibrium=120 km; zc: Thickness of the continental crust = 40 km; g: gravitational acceleration=10 m.s-2; ρw: density of sea water=1000 kg.m-3; ρco: density of the continental crust=2700 kg.m-3; ρlm: density of the lithospheric mantle =3330 kg.m-3; ρam: density of the asthenospheric mantle =3310 kg.m-3; nb: We assume here that densities are temperature independent. |
||||||||
| nb: | ||||||||
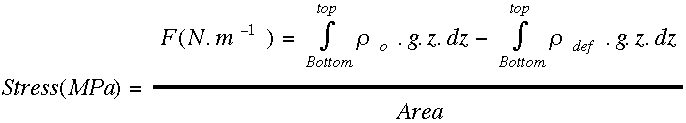 |
||||||||