Behavior of natural polycrystalline rocks
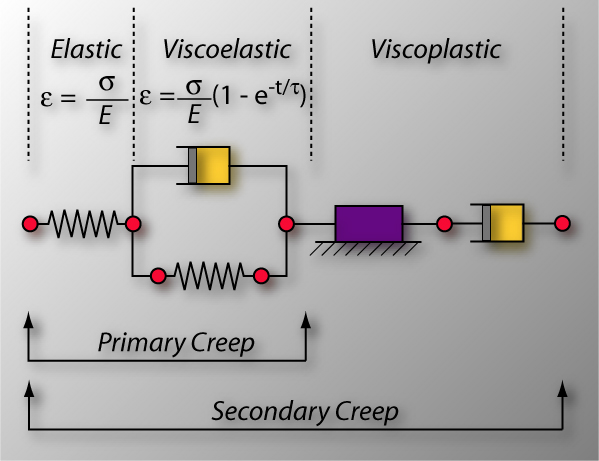
Real rocks display a complex elasto-visco-plastic behavior. This mechanical behavior can be represented by a combination of springs (elastic component), blocks on a rough surface (plastic component), and dashpots (viscous component). These mechanical analogues can be connected in series or in parallel to fit a real flow curve. The mechanical model presented here is a rock analogue. Such a model has the same flow curve than that presented in the previous slide. Below a depth of about 10 to 20 km, depending of the geothermal gradient, rock deformation is characterised by creep that can reach a steady state and therefore can accommodate large amounts of ductile deformation. It is generally assumed that the steady-state constitutive equations, or flow laws, can be used to characterise the large-strain high-temperature ductile deformation that occurs in the Earth.

Flow laws for steady-state creep: Low to moderate-stress regime
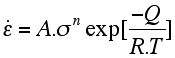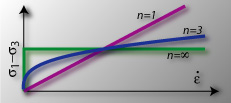
The constitutive equation that accounts for most low to moderate-stress, steady-state strain, is the power-law creep equation, so called because the absolute value of the steady-state strain rate is proportional to the differential stress raised to a power n. The following equations give the strain-rate as a funtion of the differential stress and the differential stress as a function of the strain rate:
where A is a constant (MPa-n s-1), n is the stress exponent that characterises the sensitivity of strain rate on the differential stress (n is dimensionless), Q is the activation energy per mole for the creep process (KJ mol-1), it is the energy barrier that inhibits the creep mechanism, R is the Boltzmann constant (8.3144 J mol-1 K-1), and T is the temperature (K). The constants A, Q and n are characteristic of any particular material. The power law creep shows that both temperature and differential stress have a large effect on the strain rate. Thus an increase in temperature increases the strain rate for a constant stress, or lowers the stress required to produce a given strain rate.
This effect is accounted for by the rapid increase, with increasing temperature, of the exponential term in the equations above. It can be shown that as n increases from 1 to large values, power-law material evolves from viscous material (for n=1 the power law becomes a linear relationship between stress and strain rate) to near ideal plastic material. For most rocks at moderate stress level 2<n <5, whereas at low level stress, 1<n<2.