| The geotherm in the continental lithosphere
The continental lithosphere consists in two layers with contrasted thermal properties. In particular the radiogenic heat production in the mantle is negligible compared to that of the crust. The geotherm in continental lithosphere is therefore best described by two relationships, one for the crust (equation in the previous slide), one for the lithospheric mantle.
|
|||||||||||||||||
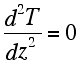 |
|||||||||||||||||
| If the production of radiogenic heat is zero in the mantle then we get: |
Integrating twice we get: |
||||||||||||||||
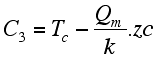 |
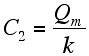 |
||||||||||||||||
| With the two following boundary conditions: T=Tc at z=zc=Moho, and Q=-Qm (the basal heat flow), we get: |
and
|
||||||||||||||||
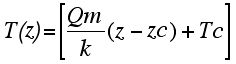 |
|||||||||||||||||
| The geotherm in the lithospheric mantle is therefore: |
|||||||||||||||||
| Hence, the geotherm in the lithosphere is defined by a two steps function: for 0<z≤zc, |
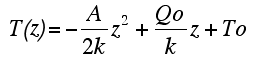 |
||||||||||||||||
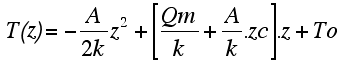 |
|||||||||||||||||
| If Qm instead of Qo is known: |
|||||||||||||||||
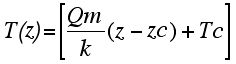 |
|||||||||||||||||
| and for zc<z≤zl, |
|||||||||||||||||
| Finally for z>zl the geotherm follows the adiabatic gradient ~0.3 K per kilometer. | |||||||||||||||||