| The geotherm in the continental crust We derive here the equation for the steady state continental geotherm. For a steady state geotherm we get that dT/dt=0 and uz =0 (no convection in the lithosphere and no erosion or sedimentation); therefore the heat transfer equation simplifies to: |
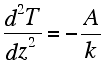 |
|||||||||||||
| This is a second order differential equation. This kind of equation is solved by integrating twice and by using two boundary conditions. For example we may know the temperature at the surface let's say: T=To at z=0; and we may know the surface heat flow for instance at z=0 the heat flow is -Qo (remember this is positive). Assuming that A is constant with depth, the first integration led to the temperature gradient dT/dz: This gives the slope of the geotherm as a function of depth. From this function we get at the surface: dt/dz=C1 |
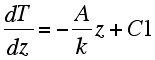 |
|||||||||||||
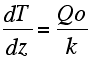 |
||||||||||||||
| The second boundary condition demands, via the Fourier's law, that at z=0: |
||||||||||||||
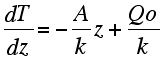 |
||||||||||||||
| by combining the last two equations for z=0 we get C1 = Qo/k, we can therefore write that... | ||||||||||||||
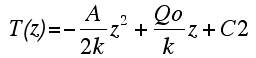 |
||||||||||||||
| Integrating a second time led to: |
||||||||||||||
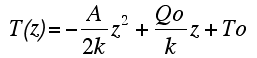 |
||||||||||||||
|
The first boundary condition says that T=To at z=0, therefore we get that: |
||||||||||||||
| This relationship is the steady state geotherm. It gives the distribution through depth of temperature in a layer with homogeneous radiogenic production A, conductivity k, with a surface temperature of To and a surface heat flow of Qo. | ||||||||||||||