| The geotherm in the continental lithosphere |
||||||
| Late in the course we will see what happens to the geotherm during and following lithospheric deformation. Here we have a glance at how sensitive is the geotherm to the rate of radiogenic heat production, mantle heat flow, conducvity and thickness of the crust. | ||||||
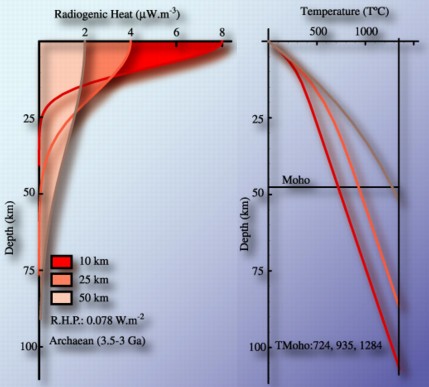
| Distribution of radiogenic heat production
We have assumed so far that the volumetric radiogenic heat production A was depth-independent ( A remains constant with depth). However, because the upper crust is enriched in incompatible elements*** the radiogenic heat production decreases with depth. A common model assumes that A is divided by e (=2.71) every h metres, h being the length scale of the exponential law. This model of distribution is given by: A(z) = A0 . Exp[-z/h] The graphs on the right shows the geotherm for A decreasing exponentially with various length scale h (10, 25, 50km). Ao is adjusted so that the total radiogenic heat production (R.H.P which is given by the integration of the radiogenic heat profile with depth) is the same in all models. The larger is h (i.e. the deeper are the radiogenic elements) the hotter is the geotherm. This suggests that at an early stage of the Earth evolution (before the extraction of the crust) the Earth had a warmer geotherm.
*** NB: these are elements that tend to concentrate into the melt phase during partial melting. Due to the buoyancy of the melt phase, incompatible elements concentrate over time into the upper part of the crust. Incompatible elements such as U, Th and K have a large radius and therefore do not fit easily into crystals lattice, hence their tendency to move into the melt phase when partial melting occurs |
 |
|||||