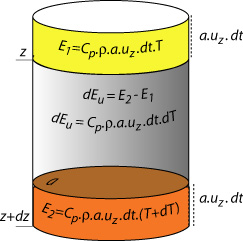
geos3003- The Dynamics of Continents & Basins


	Heat Advection Advection of heat implies that an amount of material at temperature T (in yellow on the sketch on the right) is being pushed out of our cylinder and replaced by an equivalent amount of material at temperature T+dT. The increment of heat gained or lost (dE_u) over an increment of time dt is proportional to the mass of material displaced (ρ.a.u_z.dt), the heat capacity of the material (Cp, J kg^-1 K^-1: the amount of energy required by 1kg of the material to increase its temperature by 1 K), and the temperature contrast of the two exchanged volumes. (NB: because z increasing with depth, u_z is negative for upward convection, however, dEu is a gain for upward convection hence the sign - insures that when u_z is negative (i.e. upward motion) the advective heat is positive). We get that the rate of heat advection is:

	Total heat gained or lost Adding up the rate of conductive heat (dE_c), the rate of convective heat (dE_u), and the rate of radiogenic heat (dE_r) gives the total rate of heat gained or lost. This variation of heat triggers a change in temperature dT. Since dT = dE/(Cp.m) then : Cp.m. dT= dE_r + dE_u + dE_c and:

	Which leads to the 1D conduction-advection heat transfer equation:


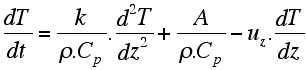	This equation describes the variation of temperature with depth and through time due to heat conduction, heat advection and radiogenic heat. This equation assumes no lateral heat flow (hence 1D). On the right end side of the equation the three terms are, from left to right, the conduction term, the term of radiogenic heat production, and the advective term. In 3D, this equation becomes:
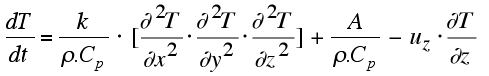