| Heat conduction Conduction transports heat from hot to cold regions. The flow of heat (Q) is proportional to the negative temperature gradient (dT/dz) between the cold and the hot region, with the coefficient of proportionality being the conductivity (k). Mathematically this translates into the Fourier's law where Q is in W.m-2 and k is in W.m-1.K-1. In our reference frame, z increases downward (T(z+dz)>T(z)). Conduction occurs in the direction of decreasing temperature (i.e. dEc is a gain for upward conduction) hence the sign "-" insures that Q is positive upward (dEc is positive when T increases downward). |
 |
||||||
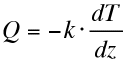 |
|||||||
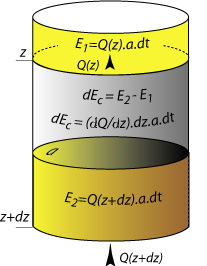
| Let's consider a small cylinder of rock of section a (area in m2). If the incoming and outgoing heat at both ends of the cylinder are the same, there is no net heat gain or loss, and the temperature remains unchanged. Temperature changes when the total heat E1 (Q(z) . a . dt) leaving the volume over a time interval dt is different to the total heat E2 (Q(z+dz) . a . dt.) entering it. The entering heat flow Q(z+dz) can be approximated with a Taylor serie in which only the two first terms are of significance. (nb: mathematically f(xn+ dx) can be approximated from f(xn) and the derivatives at location xn: f '(xn), f ''(xn), etc): |
|||||||
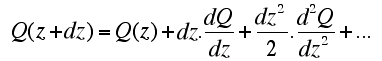 |
|||||||
| Therefore the increment of heat (dEc) gained or lost in an increment of time dt is dEc = E1 - E2 : |
|||||||
 |
|||||||
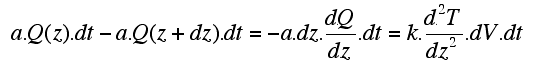 |
|||||||
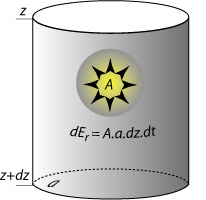
| radiogenic heat production Radiogenic desintegration of radioactive isotopes (238U, 235U, 232Th, and 40K) releases heat. The increment of radiogenic heat (dEr) produced in a small cylinder of rock of section a and length dz over an increment of time dt is: |
|||||||
|
with A the rate of radiogenic heat production. Radioactive heat is the main internal heat source for the earth as a whole (it is measured in W.m-3). |
|||||||