|
|
|
Forces, Tractions and Stresses. |
|
|
|
 |
|
|
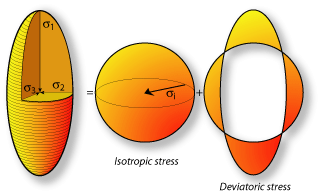
The state of stress acting on any point in the Earth's is characterized by a stress ellipsoid. The simplest stress ellipsoid is a sphere: σ1=σ2=σ3. In such a case, the stresses are the same in all directions and the state of stress is isotropic. Such a state of stress is also said to be hydrostatic or lithostatic. The magnitude of the stress (the radius of the sphere) is simply the pressure related to the weight of the column of rock above the considered point. This pressure, often called the confining pressure, comes with the same intensity from all direction and its magnitude is given by: (ρ.g.z)
When the state of stress is anisotropic, the stress ellipsoid can be decomposed into an isotropic component of magnitude σi=1/3.(σ1+σ2+σ3), and a deviatoric component that accounts for the difference between the total stress and the isotropic component. Only the deviatoric component is responsible for deformation. |
|
|
|
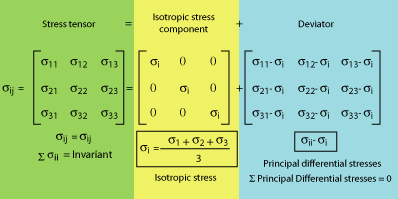
Mathematically the state of stress is a 2nd order tensor (9 components). This tensor is symmetric (σij=σji) and the sum of its diagonal components (Σσii=constant) is invariant (the value of each component changes as one changes the coordinate system, however Σσii is independent of the coordinate system). This tensor can be decomposed into an isotropic component and a deviator. It is always possible to choose a coordinate system so that the tensor is reduced to its principal stress components: ie: σij=0, and σ11=σ1, σ22=σ2, σ33=σ3. |
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|