|
|
|
Forces, Tractions and Stresses |
|
|
|
 |
|
|
The concept of Stress: Stresses can act either on physical points or across surfaces. Stress acting on a volume is described by the stress acting on each point in that volume. A stress acting across a surface corresponds to a couple of traction acting on the opposite sides of the surface. A stress acting on a surface is therefore represented by a couple of traction vectors having similar magnitudes (i.e. length) but opposite directions. This stress can be decomposed into shear components (shear stresses, τ), and normal components (normal stresses, σn). Unbalanced traction acting on a surface does not give rise to stress; it causes acceleration. Hence, the concept of stress applies to a body at equilibrium, - in a state of rest or uniform rectilinear motion. |
|
|
|
 |
|
|
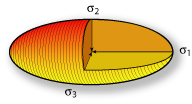
In a volume of rock, lets imagine a physical point and lets imagine a small surface centered on that point. The orientation of the small surface is characterized by its pole or "normal" n (i.e. the vector orthogonal to the surface, the length of which is proportional to the surface area). The magnitude and orientation of the stress acting on the small surface change with the orientation of the small surface. Recording the orientation and length of the stress vectors as the orientation of the small surface varies, one can see that the stress vectors define an ellipsoid centered on the point. This ellipsoid is characterized by three principal orthogonal stresses (ie 3 pairs of equal but opposite tractions) σ1, σ2 and σ3 with σ1 ≥ σ2 ≥ σ3. It can be shown that there is only three positions of the surface for which the stress is perpendicular to it, and that σ1, σ2 and σ3 are the normal stress vectors. |
|
|
| |
 |
|
|
The state of stress acting on a material point in a volume, is characterized by an ellipsoid called the stress ellipsoid. It is defined by three perpendicular axes called the principal stresses: σ1, σ2, σ3.
|
|
|
|
|
|
|
|
|
|
|
|
|