|
|
|
Strain and Strain Analysis |
|
|
|
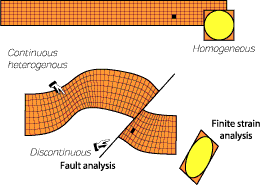
Deformation is very often partitioned between discontinuities (faults and shear zones) that limit domains where deformation is continuous (cf. sketches below). Finite strain analysis allows the characterisation of the final state of deformation (the finite strain) in domains where deformation is continuous, whereas fault analysis characterises strain associated with discontinuities. Both analyses are necessary to fully characterise finite strain fields.
The analysis of faults and shear zones consists in documenting at the local scale their orientation (strike-dip-dip direction), thickness, geometry (single discontinuity plane, anastomosed network of shear zones or brittle faults, overlapping fault segments, etc.), their kinematic and kinematic history (relative sense of displacement through time), their amount of displacement, and finally to derive the orientation of the paleostress through time that resulted in the formation of the observed fault or shear zones.
Finite strain analysis consists in measuring, at the local scale, the direction of maximum shortening and lengthening, characterising the geometry of the strain (flattening, constriction, plane strain, etc.), determining the intensity of the strain, assessing the strain history (big squeeze or a large shearing), and when appropriate determining the kinematic of the strain. |
|
|
|
The sketch on the right shows a block before and after deformation. Shortening is accommodated by a fault and rather complex but continuous internal deformation. To characterise the internal deformation of the two blocks we divide them in a number of small cells in which strain can be considered, in first approximation, as homogeneous (=> no strain gradient). When deformation is homogeneous, an imaginary sphere enclosed in each cell of the block before deformation will be transformed into an ellipsoid from which strain can easily be characterised.
Finite strain analysis is only valid when strain is considered at a scale at which strain is homogeneous. The measurement of the characteristics of strain in a large number on cells across the entire blocks fully characterises the Finite Strain Field. |
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|