|
|
|
Strain and Strain Analysis |
|
|
|
Until now we have used the words "deformation" and "strain" as if they were synonymous. They are not. The term "deformation" includes change in position, rotation, change in volume and change in shape. The term "strain" refers only to the change in shape, a synonymous term would be "distorsion". Therefore strain is only one component of deformation. In the field, translation, rotation and change in volume are difficult (but by no means impossible) to assess. Strain analysis focuses on the characterization of the change in shape. |
|
|
|
Geometric description of strain |
|
|
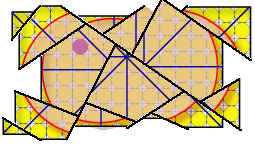
When the change in shape is related to faults and fractures (case A below) the strain is said to be discontinuous. Overall strain is assessed by the description of the network of faults and fractures and well as the rotation and translation of individual blocks.
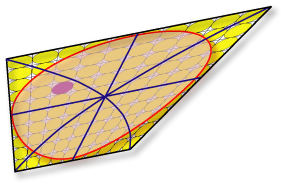
When the change in shape is related to "viscous" flow then the strain is said to be continuous (cases B and C). If the strain characteristics are the same in any location of the deformed body (i.e. no strain gradient as in case B), the strain is said to be homogeneous. In contrast, if strain varies in shape of intensity from one location to another then strain gradients exist and the strain is said to be heterogeneous (case C). |
|
|
|
Finite state C: Continuous Heterogeneous |
|
|
|
 |
|
|
 |
|
|
Initial state |
|
|
|
Finite state A: Discontinuous Strain |
|
|
|
 |
|
|
 |
|
|
| How can you distinguish between homogeneous and heterogeneous strain? |
|
|
|
Finite state B: Continuous Homogeneous |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|