| Behavior of natural polycrystalline rocks | |||||||||||||||||
| Flow Curves in the brittle regime: With pre-existing fractures At low temperature or at high strain rate or under high pore-pressure, but mainly in the upper crust and the upper mantle, the failure mechanism is modelled as frictional sliding: |
Flow Curves in the brittle regime: Without pre-existing fractures The failure mechanism is modelled by the Coulomb's criteria: |
||||||||||||||||
| where g is the gravitational acceleration, λ is the ratio of fluid pore pressure to the normal stress, ρ the density. β is a parameter dependent on the type of faulting given by: | where τ is the shear stress acting of the fracture plane, C is the cohesion between the grains at atmospheric pressure, μ is the coefficient of internal friction that characterises the roughness of the fracture plane, and σn the normal stress acting across the fracture plane: | ||||||||||||||||
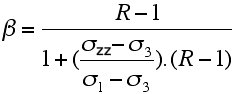 |
|||||||||||||||||
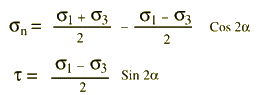 |
|||||||||||||||||
| with: | |||||||||||||||||
| where σ1 and σ3 are the largest and smallest principal stress axes. α is the angle between the fracture plane and σ1 . | |||||||||||||||||
| and μ the coefficient of internal friction. | |||||||||||||||||
| Because the coefficient of internal friction varies little around 0.75 (pretty much independent on the rock composition), we get that R=4, and therefore β varies continuously from 0.75 for normal dip slip faults, to 1.2 for strike-slip fault, to 3 for reverse dip slip faults depending of the exact value of the principal stresses ratio. The frictional sliding equation shows that it takes less differential stress to achieve brittle failure under extensional stress regime (maximum principal stress vertical) than under a compressional stress regime (maximum principal stress horizontal). This makes sense since in a compressional stress regime gravity acts against reverse faulting but enhances the principal stress in extension. | |||||||||||||||||