|
|
|
Where plates interact, rocks are subjected to stress. Stress is defined as a force per unit area. It has the dimension of a pressure (Pa). Stress is the cause of deformation.
|
|
|
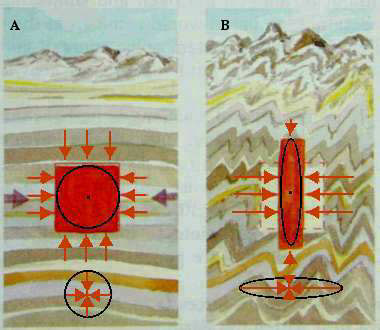
In the Earth's crust, any material point is subject to a state of stress. The point is acted upon by force vectors in every direction. In the absence of force acting on plate boundaries, the length of these vectors are the same, they define a perfect sphere centered on the point. Such a state of stress is said to be hydrostatic (Fig. A on the right). The sphere becomes larger as the material point is deeper in the crust. This state of stress is representative of the lithostatic pressure, the pressure arising because of the column of rock above.
If the crust is subjected to plate boundary forces (Fig. B on the right), the state of stress acting on each material point in the crust is no longer represented by a sphere, but by an ellipsoid charaterised by three perpendicular axis: σ1, σ2, σ3 (the principal axes of the stress ellipsoid), σ1 and σ3 being the longest and smaller axis respectively. Such state of stress is said to be non-uniform. There are two ellipses in Fig. B, the one on the bottom is a section through the stress ellipsoid, the one above represents the deformation of a volume of rock. |
|
 |
|
|
|
It is convenient to decompose a non-unifom state of stress into a uniform (hydrostatic) component, and a deviatoric component. It is only when the stress is non-uniform (i.e. when deviatoric stresses exist) that deformation occurs. Deformation is therefore related to the deviatoric component of the state of stress. Sounds complicated? Well it is! (But remember: what is good to know is hard to learn...) |
|
|
|
|
|
|
|
|
|
|