Notion of dynamics
Gravitational potential energy and gravitational force
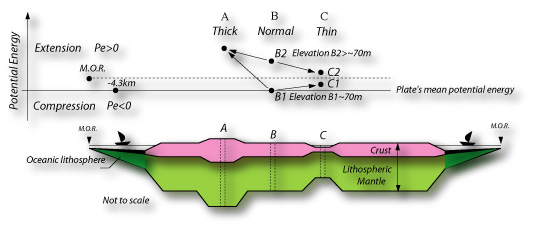
Global vs local gravitational stress field:
• The plate's mean gravitational potential energy (GPE) defines a global reference level. A lithospheric column with an excess of GPE with respect to this reference will be under extensional stresses, and under compressional stresses if it has a deficit. Continental and oceanic columns with an elevation of ~70m and -4.3 km respectively are in mechanical equilibrium with the global reference GPE. MOR have an excess of GPE which explain why they are in extension. Let's focus on the column B. Depending on its elevation, B has either an excess (B2) or a deficit (B1) of GPE with respect to the GPE of MOR. What would be evolution of the gravity-related stress acting on B during thinning which will bring the geometry of B toward that of C?

• We consider first the case where the Potential energy of column B is B1< GPE of MOR. As B becomes thinner, its GPE must increases to reach that of MOR (path B1->C1). Therefore column C is in extension with respect to its surrounding (column B). It is also in extension with respect to the global Earth's lithosphere since C has a GPE C1 greater than that of the global mean potential. Hence, the regional gravity-related state of stress enhances the global gravity-related state of stress.
• In contrast, if the column B has a GPE B2 then thinning of B will lead to a decrease in GPE (path B2->C2) . With a GPE C2, column C is in compression since it has a deficit of GPE with its immediate surroundings (B2). This regional compression opposes the global extensional state of stress related to the Δ GPE between the thinned lithosphere (C2) and the global mean potential.
• From this analysis we can define two gravitational stress field components: The Global Gravitational Stress Field (GGSF), and the Regional Gravitational Stress Field (RGSF). The GGSF results from Δ GPE between a lithospheric column and the global mean potential energy, whereas the RGSF results from the contrast in Δ GPE between a deformed lithospheric column and its immediate surrounding. The Effective Gravitational Stress Field (EGSF) is the superimposition of both gravitational stress field.