| Transient geotherms |
|||||||||||||
| Calculation of steady state geotherm is relatively straightforward as they are not time dependent. Calculation of transient geotherms, such as those displayed in slide 8 to 11, requires computational trickery as the temperature changes in both space and time. Many analytical solutions have been proposed for a range of problem. The well-known book from Carslaw and Jagger first published in 1946 "Conduction of Heat in Solids" provides hundreds of analytical solutions to many problems. Here, we give a few of them. | |||||||||||||
| Instantaneous heating or cooling The formation of oceanic lithosphere at mid-oceanic-ridge is a thermal problem involving the progressive cooling of the asthenosphere. The temperature at the seafloor Ts is maintained constant, so is the temperature in the asthenosphere Tm. The lithosphere becomes cooler and therefore thickner as cooling proceeds. Assuming no heat production and no sedimentation the 1D advection-conduction heat transfer equation becomes: |
|||||||||||||
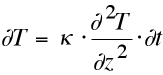 |
|||||||||||||
| with κ the diffusivity, K = κ.Cp.ρ |
|||||||||||||
 |
|||||||||||||
 |
|||||||||||||
| Th analytical solution of this differential equation is: |
|||||||||||||
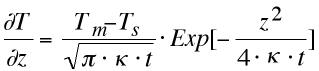 |
|||||||||||||
| By differentiating with respect to z one get the temperature gradient ... | |||||||||||||
| ...from which the variation of the surface heat flow through time can get extracted as: | 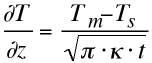 |
||||||||||||
| In the 19th century, Lord Kelvin used this last relationship to find out the age of the Earth. Kelvin made the assumption that the Earth had formed as a molten body at the temperature at which basalt melts (he assumed Tm=2000ºC) and that it had cooled by conduction to its present surface heat flow (he assumed Q0= -30 10-3 W.m-2). He considered the Earth to be spherically symmetric, and assumed that all heat was lost at the surface by conduction (with κ =10-6.m-2.s-1). Thus the problem is reduced to that of finding the temperature within a cooling half-space of infinite extent as a function of time after the half space is set at a specific temperature, a problem for which the equations above apply. Kelvin found that the Earth was 50 Myr old... |
|||||||||||||