| Plate tectonic forces: | |||||||||
| Maximum resulting tectonic force: The Slab Pull | |||||||||
| A simple formulation for the slab-pull per unit length parallel to the trench is given by : Vslab Δ ρ g. This formulation assumes that the density of the plate and that of the asthenosphere are temperature-independent. Assuming an average density contrast of about 50 kg m-3, a depth of the subducting slab d = 600 km, a thickness of the slab t = 100 km and g = 10 m s-2, we get an absolute maximum for the slab pull Fsp ~ 3×1013 N m-1. Note: the value would be an order of magnitude greater (Fsp ~ 1.5×1014 N m-1) for a slab going all the way down to the core-mantle boundary. A more accurate formulation takes into account the temperature dependence of density, the diffusion of heat, and the velocity of the subducting slab. An estimate of the slab-pull force per unit length of subduction zone, Fsp(z), acting at depth Fsp and caused by the density contrast between the cold oceanic plate and the mantle is given by: |
|||||||||
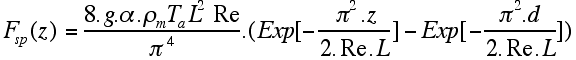 |
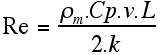 |
||||||||
| with: | |||||||||
| where Re is the thermal Reynolds number (the ratio of heat convection to heat conduction), z is the depth beneath the base of the oceanic plate, α is the coefficient of thermal expansion (3×10-5 K-1), Ta is the temperature of the asthenosphere (1350ºC), k is the thermal conductivity (2 W m-1 K-1), L is the thickness of the plate (85 km) and d is the depth of the upper mantle (d+L = 660 km), Cp is the specific heat (1.17×103 J kg-1 K-1), and v is the rate at which the oceanic slab sinks into the mantle (~ 10 cm yr-1). Using the above values we get Fsp = 2.5×1013 N m-1.
However, it is worth noting that Fsp linearly depends on the ill-defined coefficient of thermal expansion. With a coefficient of thermal expansion varying in the range of 2×10-5 to 4×10-5 K-1 the slab-pull force varies between 1.7×1013 and 3.4×1013 N m-1. In addition, the olivine-spinel phase change which occurs at around 350 to 420km increases the density in the subducting slab, providing an extra pull. Note: This extra pull depends on the thermodynamical characteristics of the phase transition, notably the slope of its Clapeyron curve (dP/dT). The value of the slope of the Clapeyron curve ranges between 3 and 4 MPa K-1. The resulting extra pull ranges between 1.2×1013 and 1.6×1013 N m-1. The slab-pull force is opposed by the friction force between the slab and the lithosphere viscosity of the asthenospheric mantle. This force is proportional to the velocity of the subducting plate and to the viscosity of the asthenosphere, that is also poorly constrained. Numerical calculations based on the differential equations for the flow of a viscous fluid suggest that the resistive force is of the order of 1013 N m-1. |
|||||||||